What is the sum of all squares, for numbers between 1 and 10 ?
Let us do this the classic way, yeah ?
1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100 = 385
Or, if you want to use numerical-methods, just use this expression below (with n=10)
Great, how about the sum of all squares between 1 and 100 ? or just the sum of squares between 21 and 30 ?
These are more painful than the one above isn’t it ?
If you do it the excel way, where you square every integer between 1 and 100 and add them up, you’d end up with 338,350
You can use numerical-methods to estimate the sum of squares between 21 and 30, but you are going to have to deduct the estimate for (1 to 20), from (1 to 30), to get the answer for 21 to 30
It’s clumsy and your chances of making a mistake is higher
There has to, has to, be a more elegant way to do all of this, right ?
Just take the integral - that’s what it exists for … that’s really what its built for
Most of the times we don’t appreciate integrals, because we simply don’t know how to use them, or more importantly, when to use them
and since we think we have no use for them, we simply ignore them
But integrals are essentially a cheat code for otherwise - you and me doin’ a ton of math
… and if its between a lot of work, and little to NO work, y’all should know by now that I’mma pick the latter, six days a week and thrice on a Sunday
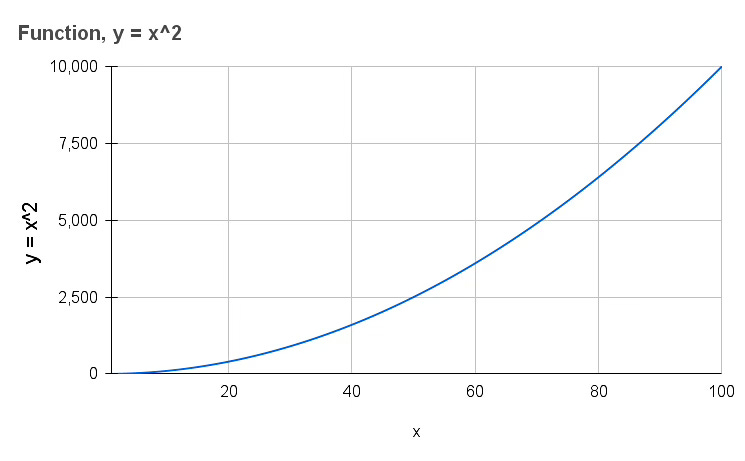
Say, in this case, let us think of this function
When you plot this and get a curve, taking the integral of this essentially means you are estimating all of the area under the curve - and that in essence is estimating the sum of all squares between 1 and 100
How mathematically elegant is that ? When we do this in excel in the brute-force way, we don’t appreciate the elegance and simplicity of integrals
The only thing you need to find out is the integral for x^2. Essentially, the integral of x^n is x^(n+1)/(n+1)
So, in our case,
These are just calculus rules - when you want to integrate an expression, you can just ask google and it would tell you what your integral for that function is, and then you are off to the races
You just solve this equation above for 100 as the upper limit and 1 as the lower limit, and deduct the latter from the former
So, because this integral has a definite upper and lower limit, we call these definite integrals, and in the case of definite integrals, the C from above goes away, as in - it does not have any relevance to the final result
You can easily do this between any interval, such as 21 to 30, or 41 to 50 - and this is hard to do in the numerical-methods expression above
Integrals are just cleaner - for problems such as these
Great, the actual answer (as I mentioned above) is 338,350, and our answer from integrating the function x^2 between 1 and 100 is 333,333
So, your integral got you within 1.5% of the actual answer, and you didn’t need to do any excel or numerical methods, you simply could have done this in the back of an envelope
- quite literally
We use integrals in physics, engineering, math, economics, finance, and probability and statistics … they are just a cheat code to avoid doing a truckload of math
If you think about it, you can do it the discrete way, by estimating the square of each integer between 1 and 100, and adding them up to get to your answer
or in a case where you understand the form-function of the curve (and in this case, you do, you know exactly what x^2 looks like, for each value of x between 1 and 100)
then you plot y (x^2) as function of x, and simply take the area underneath the curve
This is the whole reason why we created integrals for, we call these Riemann Sum … its essentially integral calculus
Next time, when someone gives you a painfully large range over which you need to repeat the same mathematical operation over and over again - like taking the square of all integers between 1 and 100, and adding them
Let it marinate for a second and think about if there is a mathematically more elegant way to solve it - that is also easily scalable
You can either write a for-loop in python, or simply, take the integral
And, get comfortable in getting close to the answer within a reasonable margin of error, and be confident enough to defend it
Our world is filled with people who think estimating the weight of a cotton-candy to the ninth decimal place is of paramount importance … before they go home. Its really more about their insecurities and fear than yours - that they make you do it
because, you know, people who are hardwired to do deterministic math, their brains would fritz out if you introduce likelihoods, stochastics, probabilistic outcomes and concepts such as - within a reasonable margin of error
Beautiful !
Well … screw ‘em
If you aren’t developing coordinates to land on the moon, then a deviation of 1.5% works in most normal cases
And if someone complains about the 1.5% - take an obscenely oversized bucket of gatorade and empty it on them, and this here is important, I’d highly prefer it if you do it in the middle of the conference room table and walk out
‘tis January, ‘tis sports … ‘tis football
… I’m just gettin’ warmed up
Gun Far, Trips Right, Fake 60, Flounder Left … White 20-SET !

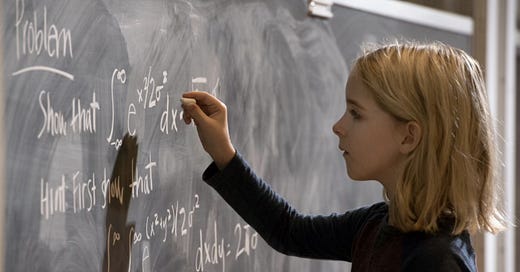


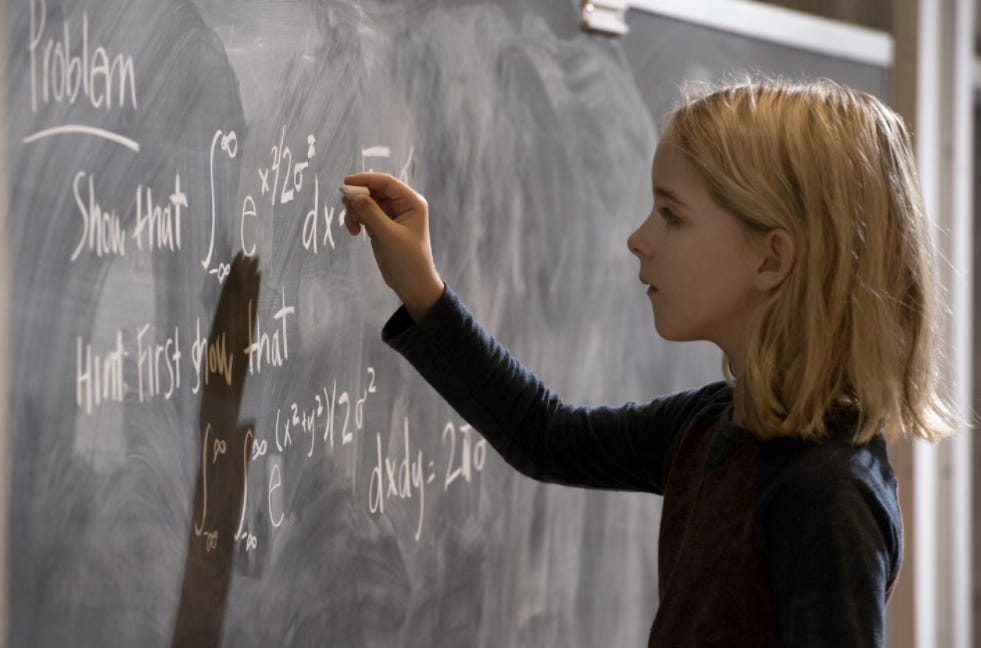

:) You failed to highlight the important part, "google the integral" When I was learning calculus back in the paleosilicate age, there was no Google. Yes, there were tables of integrals but no guarantee that the integral you wanted was in the table without clever trmsfrmation of the problem.